В сети появилась задачка, вызвавшая множество споров среди пользователей. Любитель парадоксов Тим Урбан предложил задачу с тремя конфетками, которую большинство пользователей оказались не в состоянии решить.

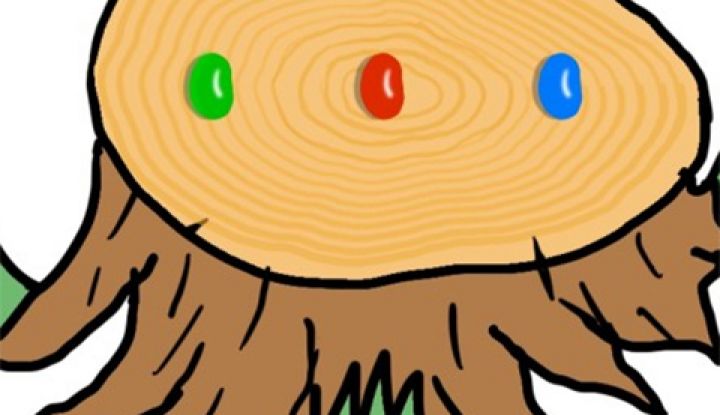
Формулировка задачи: странника обвиняют в краже и предлагают решить свою судьбу, выбрав из трех конфет. Две из них ядовиты. Путник берёт конфету, например зелёную, обвинитель забирает ещё одну из оставшихся на пне, к примеру синюю, сообщая, что она точно ядовита.

В руках героя конфета, ещё одна — на пне. До того, как съесть конфету, игрок может поменять конфету. Вопрос: стоит ли путнику менять свой выбор? С математической точки зрения вопрос сводится к тому, какова вероятность выигрыша, если игрок сменит выбор после того, как обвинитель уберёт одну из конфет.

Большинство решающих задачку считают, что в обоих случаях, если путник меняет или не меняет выбор, вероятность остается 50% на 50%. Неверно. С математической точки зрения, вероятности распределяются по-другому.

Урбан переиначил парадокс Монти Холла. Этот парадокс был использован в телевизионном шоу под названием «Бьёмся об заклад» («Let’s Make a Deal»), в котором игрокам предлагали выиграть автомобиль, если они сделают правильный выбор из трех дверей. За двумя из них скрывались козы, в то время как за третьей — автомобиль. Ведущий так же, как и в случае с конфетами, предлагал игрокам поменять свой выбор после того, как открывал одну из дверей.

Как мы выяснили, решить задачу становится проще, если представить, что на пне находится не 3 конфеты, а например 1000. Когда игрок выбирает одну конфету, ведущий убирает оставшиеся 998 конфет, заявляя, что все они отравлены.

Поразмыслите над задачей сами, а для самых нетерпеливых редакция Bomba.co оставляет подсказку с объяснением математической стороны дела.